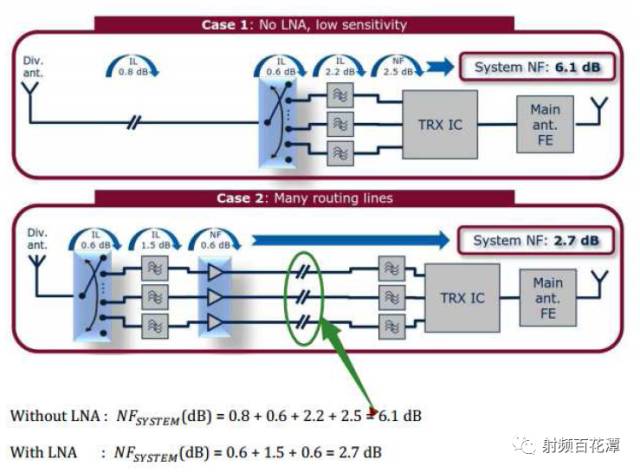
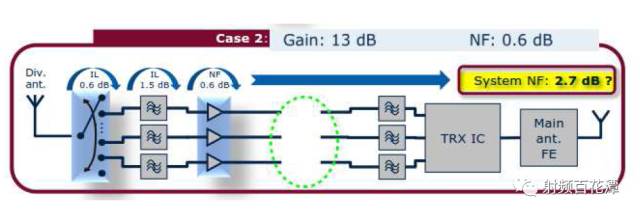
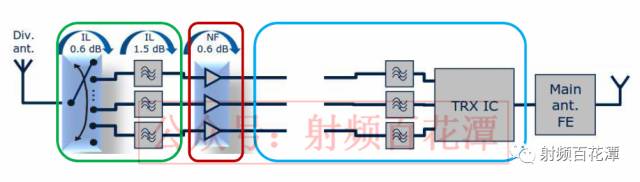
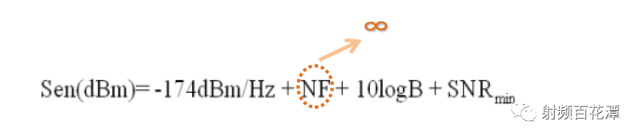
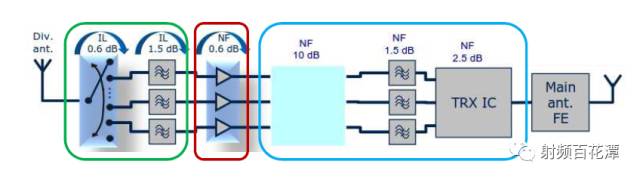
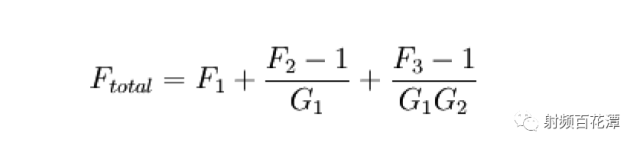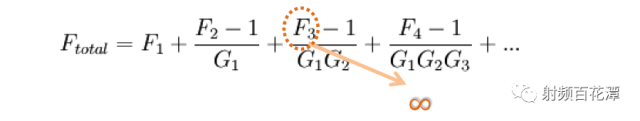Does the insertion loss behind the low noise amplifier LNA have any effect on sensitivity?

Does the insertion loss behind the low noise amplifier LNA have any effect on sensitivity?

Why did Xiaobian ask such a question, did not learn the noise cascade formula?

In the following way, I add a 10db attenuation between the LNA and the IC, and the impact on the receiving sensitivity is also small?

It is seen from the above that NFsystem is reduced by 6.1-2.7=3.4dB.

That is, the sensitivity is improved by 3.4dB.

Let me start by saying whether the Loss behind the LNA is much smaller than the Gain of the LNA.

Yes => No effect

No => Influential

First ask a question if Loss after LNA does not affect sensitivity

Then after LNA Open (also known as Loss infinity) as shown below:

Is it possible that sensitivity is not affected?? Your first instinct is impossible.

Yes, because you can't receive sensitivity even with the signal??

To explore whether Loss after LNA will affect sensitivity

You must first know how much Loss affects sensitivity after LNA.

According to the NF cascading formula and Friis Formula:

In fact, the calculation only needs to use LNA as the watershed.

Can be simplified into three blocks as shown in the green frame, red frame, basket

Calculated its NF is 3 dB

The LNA's Gain is assumed to be 13 dB, which is G2 with 19.95.

You can see that when G2 = 19.95 is brought into the denominator

Almost negligible

Actually

LNA's Gain will dilute the contribution of the LNA rear block to the overall NF of the receive path.

So if we only calculate the NF sum of the green and red boxes, we get 2.7 dB.

Similar to the 3 dB calculated above

Therefore, there is a conclusion that "Loss behind LNA can be ignored"

But the focus is coming

The reason why F3-1/G1G2 can be ignored

That's because (F3-1) is much smaller than G1G2

In this case

F3-1 = 2

G1G2 = 12.3

F3-1/G1G2= 0.16

Conversely if (F3-1) is not much smaller than G1G2

F3-1/G1G2

Not negligible

To ask the question as an example after LNA Open

That is, F3 is infinite, and it is substituted into Friis Formula:

The NF of the overall receiving path becomes infinite

According to the sensitivity formula, the NF infinity of the overall receiving path is substituted into the formula:

That is, your sensitivity is infinite

There will be no infinite signal in this world, so that your receiver will not receive the signal completely.

So when you (F3-1) are not much smaller than G1G2

Loss behind the LNA definitely has an impact on sensitivity

It is also confirmed by the formula that your first intuition is correct.

Open sensitivity cannot be affected after LNA

So go back to your initial question

"Adding a 10 db attenuation between the LNA and the IC has little effect on the receiving sensitivity? 』

We have to calculate whether this (F3-1) is much smaller than G1G2 after adding this 10 dB attenuation.

F3-1 = 24

G1G2 = 12.3

Obviously (F3-1) is not much smaller than G1G2

So this 10 dB attenuation definitely has an impact on sensitivity.

Calculated that the NF of its overall receive path is 5.82 dB

The NF just calculated without this 10 dB attenuation is 3 dB

In other words, after you add this 10 dB attenuation

Its sensitivity is degraded by 5.82 – 3 = 2.82 dB, so it has an effect

Of course you will say if the LNA of LNA is bigger, the better.

The more you can make this

Is the condition that "Los behind LNA is much smaller than Gain of LNA"?

In theory, this is true.

But actually the LNA's Gain is too big.

The rear circuit will be saturated by the signal output by LNA Output.

Its Noise Floor rises, the SNR decreases, and the sensitivity is still not good.

Moreover, the larger the Gain of the LNA, the smaller the IIP3 of the overall receiving path will be.

Once there are more than two external interference signals, the larger the IMD3 will be generated

Because this IMD3 is very close to the RX signal, your SAW Filter can't filter it.

As a result, IMD3 will increase the SNR of the Noise Floor of the RX signal.

That sensitivity is still not good

Bad linearity will also produce poor sensitivity.

So the LNA of LNA is not as big as possible, not as small as possible, but just better.

It is also known that even if the LNA can make the Loss behind it, it does not affect the sensitivity.

But if the Loss behind it is too large, it will affect the sensitivity.

That is, the degree of sensitivity of the LNA will be greatly reduced.